• Location
    Schorenstrasse 39,
    3645 Gwatt (Thun), Switzerland
  1. Home
  2. Ultra High Strain Rate Testing

ULTRA HIGH STRAIN RATE

High strain rate testing of materials remains largely unexplored due to the limitations in conventional nanoindentation instrument design where the resonance frequency of the system is commonly too low to allow for high strain rate experiments. Although the nanoindentation technique has evolved in recent years, most tests are still typically performed in the quasi-static regime, meaning at strain rates in the range of 10-5 to 10-2 s-1. However, high strain rates above 10-2 s-1 have remained unexplored.

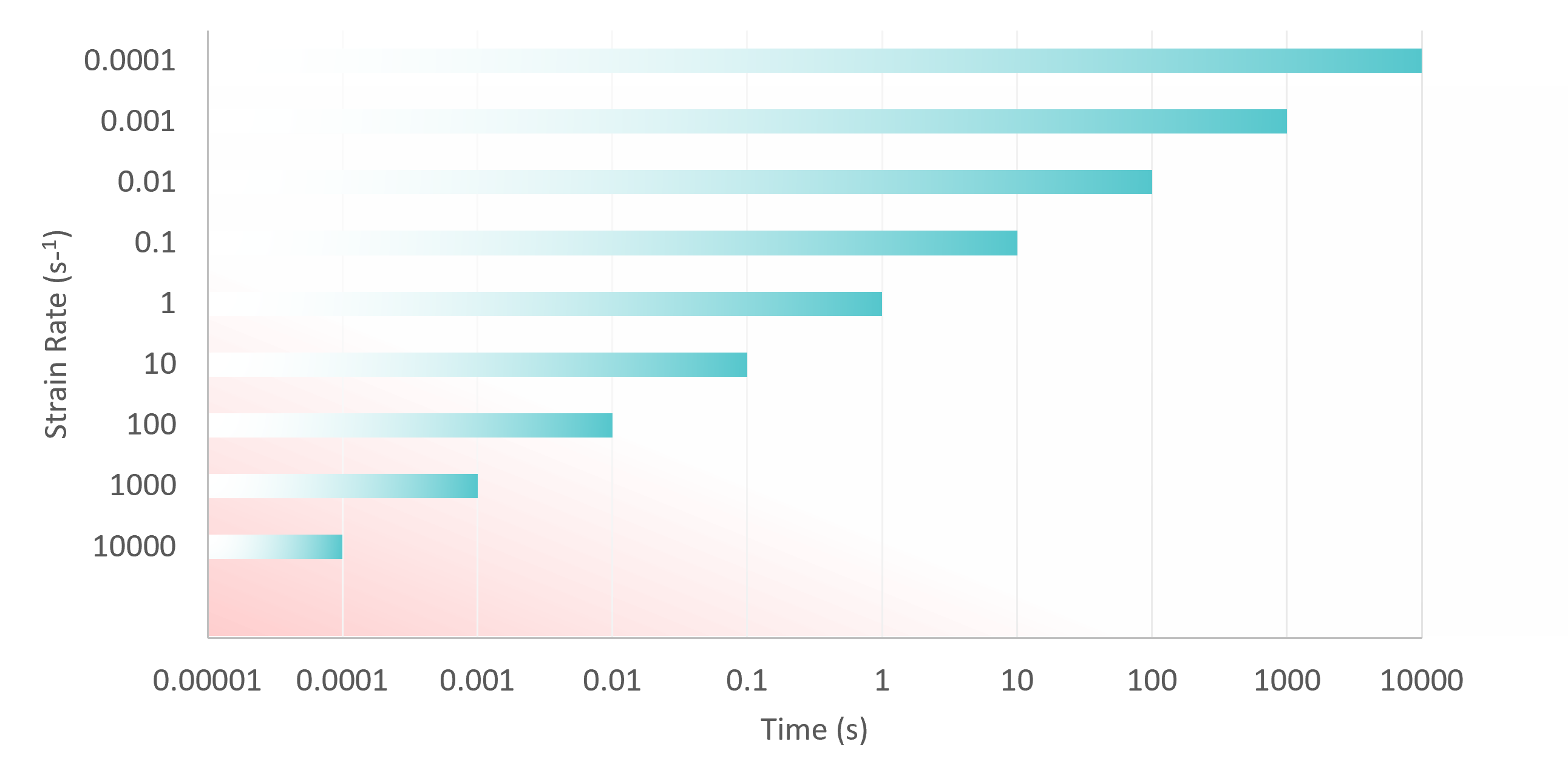
Strain rate (s-1) is the inverse value of the time it takes to perform the mechanical loading. As a result, experiments take as little as 0.1 ms at maximum strain rates. The Alemnis High Strain Rate modules enable experiments across 9 orders of magnitudes!

Performing high strain rates testing of materials to understand their behavior is of great interest, both in industrial applications and in fundamental research. Some industrial examples include the impact resistance of ballistic armor, survival of components/devices when dropped, crash testing, metalworking operations, etc.  From a scientific viewpoint, being able to test materials over a wide range of strain rate including high strain rate testing allows the deformation mechanisms to be probed and understood, particularly with regard to determination of activation volumes.

Nine orders of magnitudes of strain rates for indentation, tensile- and compression testing makes Alemnis the world’s fastest micro mechanical testing system, enabling unprecedented extreme experiments.

Alemnis provides the only high strain rate system that offers:

  • Constant and controlled strain rates
  • Continuous testing from quasi-static to high strain rates
  • Read-out frequency of 1 MHz for displacement and load.
  • Direct data analysis without complicated modeling or system assumptions

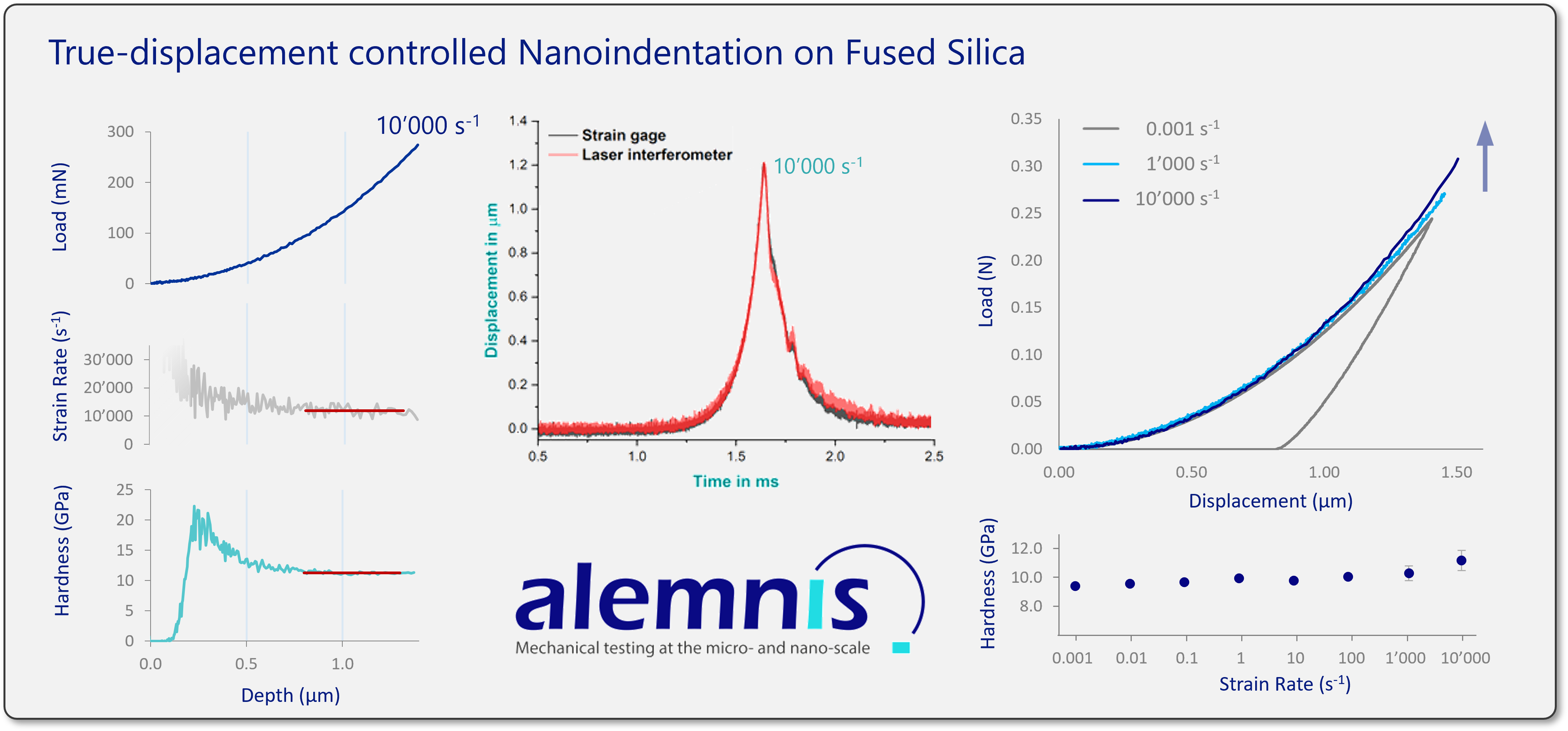
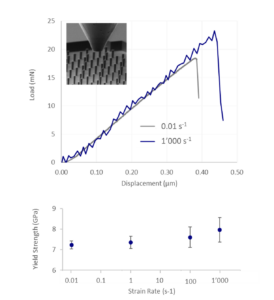
Nanoindentation on fused silica across 8 orders of magnitudes of strain rates confirms small but measurable hardening effect, consistent with literature [1]. At strain rates above 100 s-1, hardness is calculated using the contact stiffness obtained at quasi-static conditions. This widely accepted method circumvents the issue of missing unloading curves at extreme strain rates.

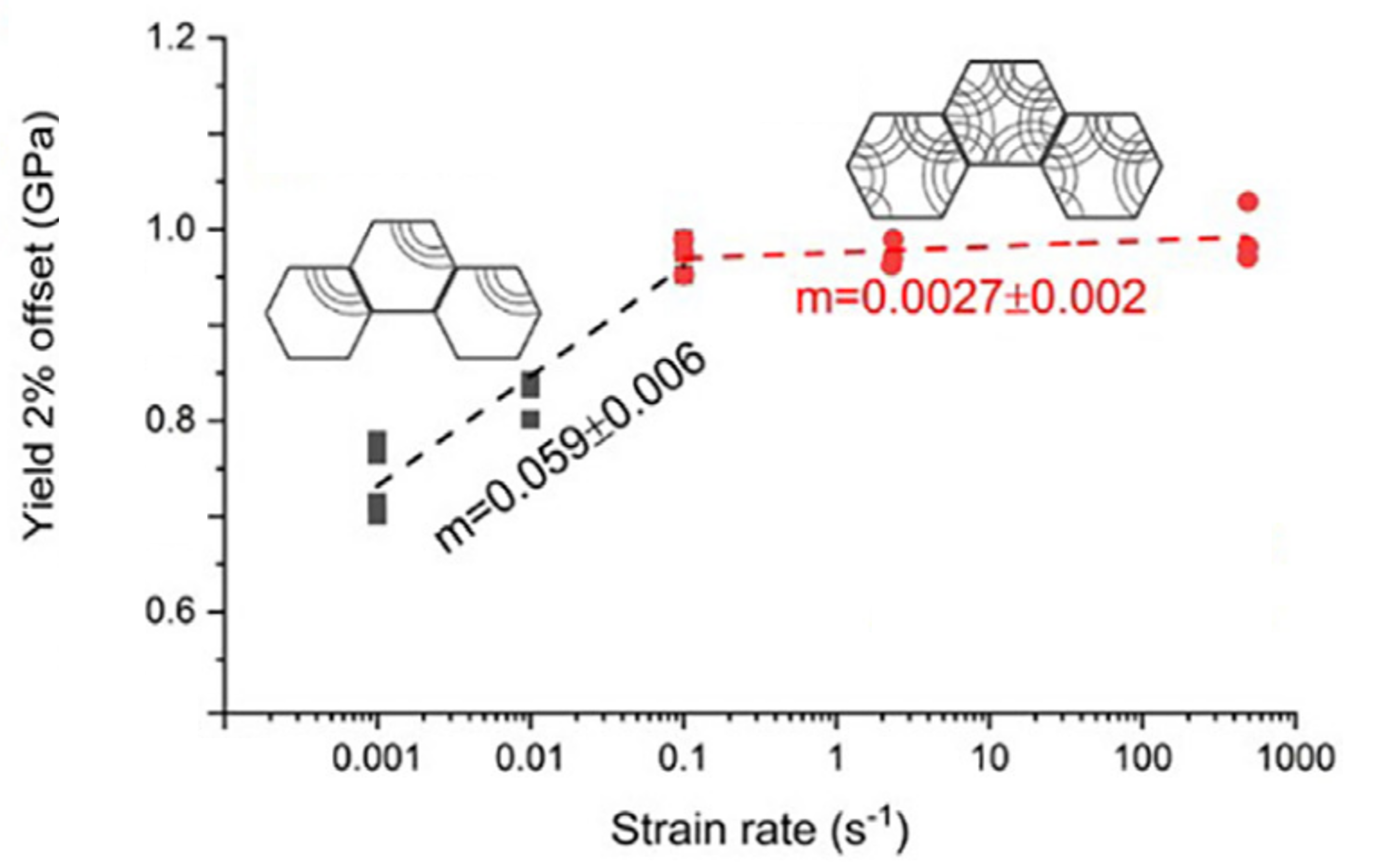
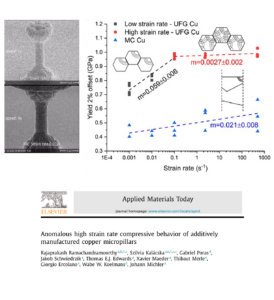
High strain rate compression of additively manufactured copper micropillars. [10]

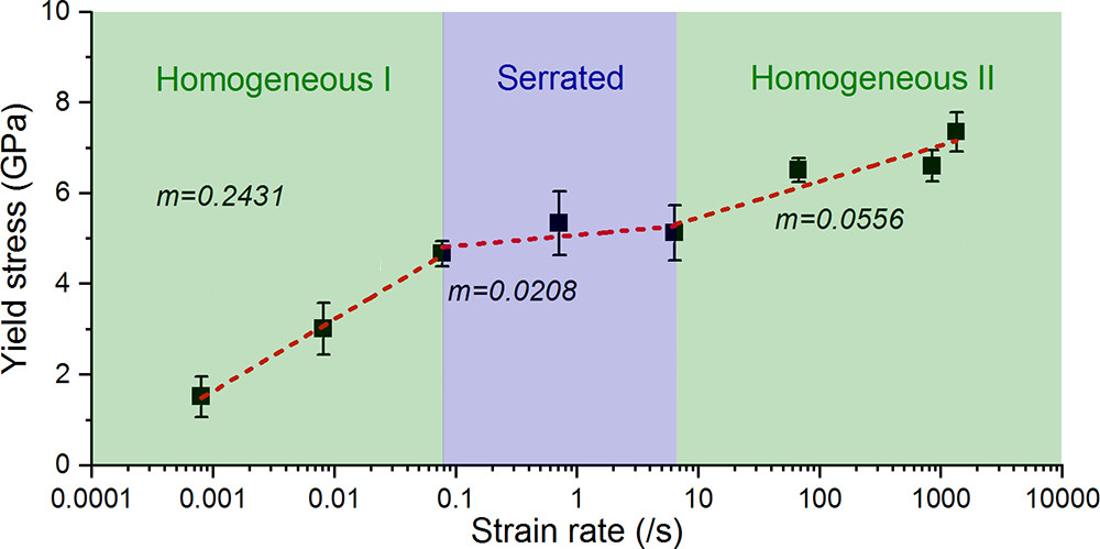
High strain rate compression of fused silica micropillars. [19]

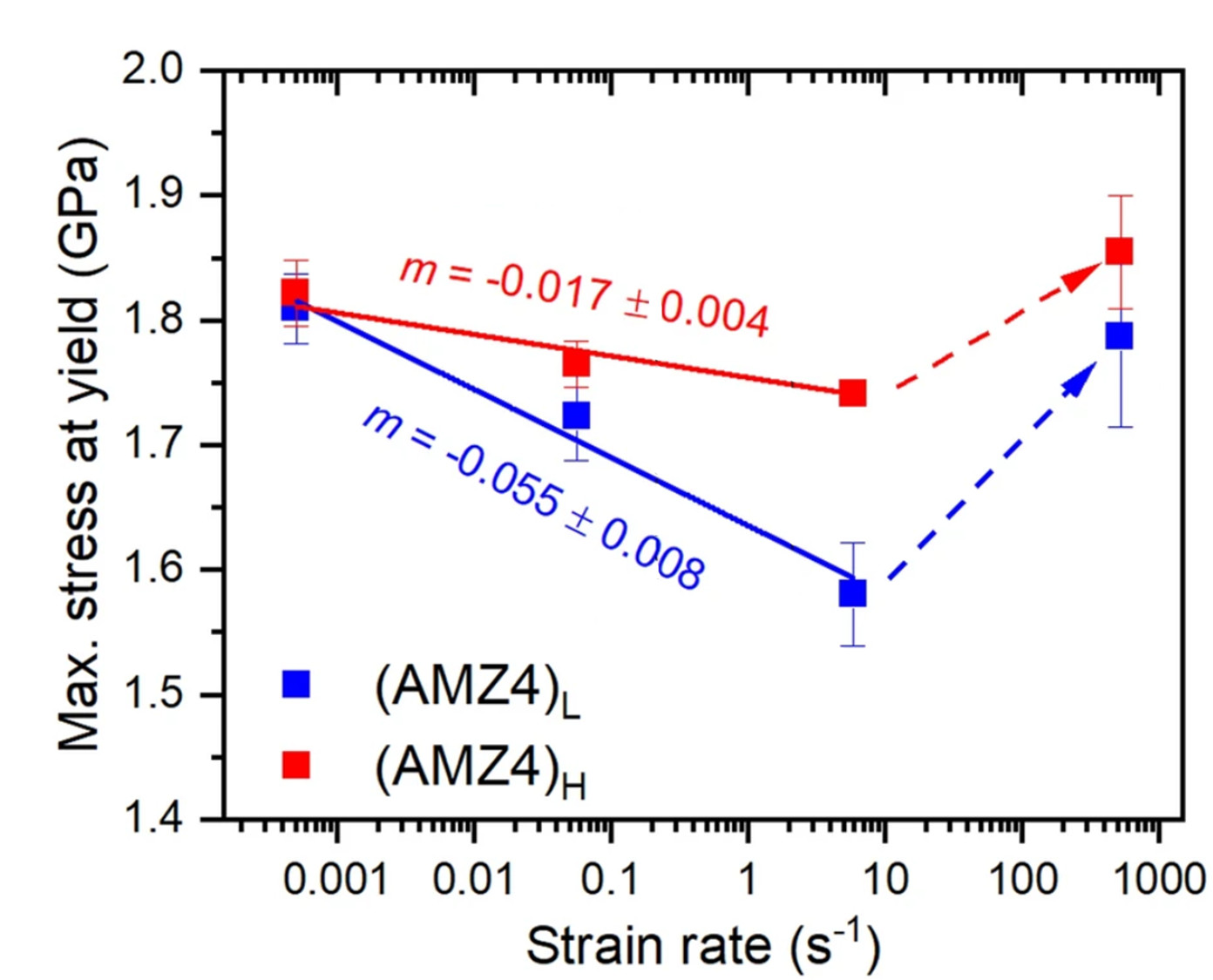
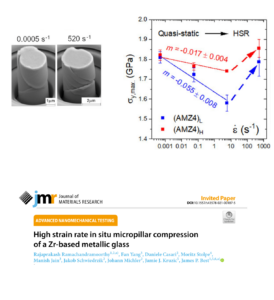
High strain rate compression of micropillars of bulk metallic glass. [13]

More Application Examples

Metamaterials

https://doi.org/10.1038/s41586-023-06652-x

Ceramics

https://doi.org/10.1002/adma.202303142

Glasses

https://doi.org/10.1021/acs.nanolett.8b05024

Metal-Organic Frameworks

https://doi.org/10.1021/jacs.1c08368

Biomechanics

https://doi.org/10.1016/j.actbio.2021.07.005

Additive Manufacturing

https://doi.org/10.1016/j.apmt.2022.101415

Metallic Glasses

https://doi.org/10.1557/s43578-021-00187-5

Semiconductors

Alemnis AG

Polymers

https://doi.org/10.1016/j.matdes.2020.108977

The Alemnis Standard Assembly (ASA) achieves ultra high strain rate covering 8 orders of magnitude.

The Alemnis Standard Assembly (ASA) can be configured in several ways to achieve ultra high strain rates up to 10’000 s-1, thus covering 8 orders of magnitude! Such high strain rates are possible because the dimensions of a typical micropillar are so small relative to the actuation velocity, the lower magnitude of inertial contributions and faster stress wave equilibration times.

For example, the duration of a dynamic experiment conducted at 1000 s-1 strain rate is  ̴70 µs for both macro- and microscale samples. If we take fused silica, which has an elastic wave speed of  ̴ 5823 ms-1, the wave travel time in a typical macroscale sample of 9 mm thickness (typical Kolsky bar sample thickness is 6 – 12 mm) is  ̴ 2 µs, while the wave travel time in a 5 µm high micropillar of the same material is 1 ns. Thus, at the macroscale, the experiment duration is of the same order of magnitude as the wave travel time, so understanding the wave propagation phenomena is vital (and in practice very complicated). On the other hand, at the microscale, the experiment duration far exceeds the wave travel time, essentially making the wave propagation phenomena irrelevant in such samples at strain rates less than  ̴ 105 s-1. Therefore, in dynamic micromechanical testing, the elastic and plastic constitutive material properties of microscale samples can be obtained at very high strain rates without interference from the elastic waves in the material. This means that exploring the high strain rate mechanical properties at the microscale is very advantageous compared to the macroscale.

See product page
Request a quote for Alemnis Standard Assembly.
Quote
FREE DOWNLOAD

Send download link to:

I confirm that I have read and agree to the Privacy Policy.

APPLICATION NOTE: Designing micropillar strain rate jump tests to study time dependent plasticity

Selected References

  1. Cherukuri, R. et al. In-situ SEM micropillar compression and nanoindentation testing of SU-8 polymer up to 1000 s−1 strain rate. Mater. Lett. 358, 135824 (2024).
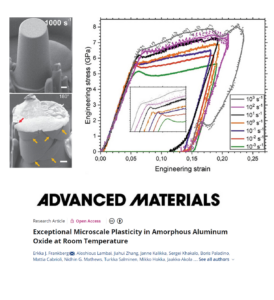
  2. Frankberg, E. J. et al. Exceptional Microscale Plasticity in Amorphous Aluminum Oxide at Room Temperature. Adv. Mater. 2303142 (2023) doi:10.1002/adma.202303142.
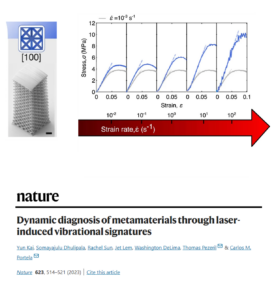
  3. Kai, Y. et al. Dynamic diagnosis of metamaterials through laser-induced vibrational signatures. Nature 623, 514–521 (2023).
  4. della Ventura, N. M. et al. Micromechanical response of pure magnesium at different strain rate and temperature conditions: twin to slip and slip to twin transitions. Acta Mater. 243, 118528 (2023).
  5. Ventura, N. M. della et al. Response of Magnesium Microcrystals to C-Axis Compression and Contraction Loadings at Low and High Strain Rates. SSRN Electron. J. 118762 (2022)
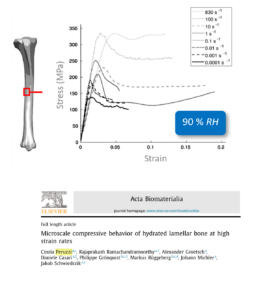
  6. Peruzzi, C. Nanoscale Deformation Mechanisms and Yield Prediction of Lamellar Bone. at https://doi.org/10.3929/ethz-b-000574773 Rights (2022).
  7. della Ventura, N. M. et al. Evolution of deformation twinning mechanisms in magnesium from low to high strain rates. Mater. Des. 217, (2022).
  8. Schwiedrzik, J. et al. Dynamic cryo-mechanical properties of additively manufactured nanocrystalline nickel 3D microarchitectures. Mater. Des. 220, 110836 (2022).
  9. Widmer, R. N. et al. Temperature–dependent dynamic plasticity of micro-scale fused silica. Mater. Des. 215, 110503 (2022).
  10. Ramachandramoorthy, R. et al. Anomalous high strain rate compressive behavior of additively manufactured copper micropillars. Appl. Mater. Today 27, 101415 (2022).
  11. Guillonneau, G. et al. Plastic Flow Under Shear-Compression at the Micron Scale-Application on Amorphous Silica at High Strain Rate. Jom 74, 2231–2237 (2022).
  12. Ventura, N. M. della et al. Unconventional Deformation Twinning Mechanisms in Magnesium at High Strain Rates. SSRN Electron. J. 1–25 (2021)
  13. Ramachandramoorthy, R. et al. High strain rate in situ micropillar compression of a Zr-based metallic glass. J. Mater. Res. 36, 2325–2336 (2021).
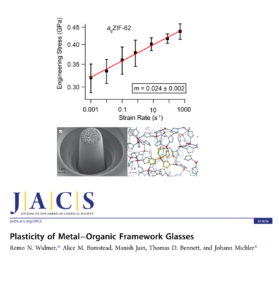
  14. Widmer, R. N. et al. Plasticity of Metal-Organic Framework Glasses. J. Am. Chem. Soc. 143, 20717–20724 (2021).
  15. Lin, Z. et al. In-Situ SEM High Strain Rate Testing of Large Diameter Micropillars Followed by TEM and EBSD Postmortem Analysis. Exp. Mech. 61, 739–752 (2021).
  16. Peruzzi, C. et al. Microscale compressive behavior of hydrated lamellar bone at high strain rates. Acta Biomater. 131, 403–414 (2021).
  17. Breumier, S. et al. High strain rate micro-compression for crystal plasticity constitutive law parameters identification. Mater. Des. 193, 108789 (2020).
  18. Rohbeck, N. et al. Effect of high strain rates and temperature on the micromechanical properties of 3D-printed polymer structures made by two-photon lithography. Mater. Des. 195, 1–9 (2020).
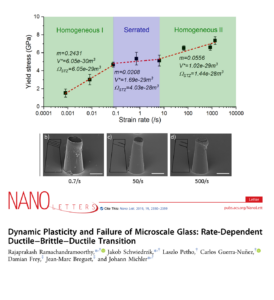
  19. Ramachandramoorthy, R. et al. Dynamic Plasticity and Failure of Microscale Glass: Rate-Dependent Ductile-Brittle-Ductile Transition. Nano Lett. 19, 2350–2359 (2019).
  20. Guillonneau, G. et al. Nanomechanical testing at high strain rates: New instrumentation for nanoindentation and microcompression. Mater. Des. 148, 39–48 (2018).